Mapping technique
The generation of L4 products in DUACS is based on different techniques depending on the product considered:
- Copernicus Marine Service products: L4 product generation is based on the Multiscale Inversion of Ocean Surface Topography (MIOST) mapping approach, as described in Ubelmann et al., (2021a, 2022). This method is able to account for various modes of variability of the ocean surface topography (e.g., geostrophic, barotrope, equatorial waves dynamic, etc. ) by constructing several independent components within an assumed covariance model. .In these products, we have focused on different modes (geostropic, barotropi,…). Table describes the modes for each product.
- C3S products: L4 product generation is based on a simple optimal interpolation method as described in Le Traon et al, 1998a; Pujol et al, 2016. The signal reconstruction is constrained by a single-scale covariance function Arhan and De Verdiére, (1985); Le Traon et al.,( 1998a) and primarily focus on geostrophic circulation (processes with typical space and timescales greater than 100 km and 10 days)
Table : Description of the different modes of variability of ocean surface topography for each product
| Product Name | Product ID
Dataset ID |
Spatial coverage | Temporal coverage | L3 Input data | MIOST components | Source |
| Global Ocean Gridded L 4 Sea Surface Heights And Derived Variables Nrt | SEALEVEL_GLO_PHY_L4_NRT_008_046
cmems_obs-sl_glo_phy-ssh_nrt_allsat-l4-duacs-0.25deg_P1D cmems_obs-sl_glo_phy-ssh_nrt_allsat-l4-duacs-0.125deg_P1D |
Global and Regional Europe | 1 Jan 2022 onwards | SEALEVEL_GLO_PHY_L3_NRT_008_044 (https://doi.org/10.48670/moi-00147) | – Geostrophy,
-Long Wave Length error |
https://doi.org/10.48670/moi-00149 |
| Global Ocean Gridded L 4 Sea Surface Heights And Derived Variables Reprocessed 1993 Ongoing | SEALEVEL_GLO_PHY_L4_MY_008_047
cmems_obs-sl_glo_phy-ssh_my_allsat-l4-duacs-0.125deg_P1D cmems_obs-sl_glo_phy-ssh_my_allsat-l4-duacs-0.125deg_P1M-m |
Global and Regional Europe | 1 Jan 1993 to 14 Jun 2024 | SEALEVEL_GLO_PHY_L3_MY_008_062 ( https://doi.org/10.48670/moi-00146) | – Geostrophy,
-Long Wave Length error |
https://doi.org/10.48670/moi-00148 |
| Global Ocean Gridded L 4 Sea Surface Heights And Derived Variables Nrt DEMO | SEALEVEL_GLO_PHY_L4_NRT_008_046
cmems_obs-sl_glo_phy-ssh_nrt_demo-allsat-swos-l4-duacs-0.125deg_P1D-i cmems_obs-sl_eur_phy-ssh_nrt_demo-allsat-swos-l4-duacs-0.0625deg_P1D-i |
Global and Regional Europe | Nov. 2025 to onwards | SEALEVEL_GLO_PHY_L3_NRT_008_044 (https://doi.org/10.48670/moi-00147)
SWOT Level 3 Ocean Products (10.24400/527896/A01-2023.018)
|
– Geostrophy,
-Long Wave Length error |
None |
| Global Ocean Gridded L 4 Sea Surface Heights And Derived Variables Reprocessed 1993 Ongoing DEMO | SEALEVEL_GLO_PHY_L4_MY_008_047
cmems_obs-sl_glo_phy-ssh_my_allsat-demo-l4-duacs-0.125deg_P1D-i cmems_obs-sl_eur_phy-ssh_my_allsat-demo-l4-duacs-0.0625deg_P1D-i |
Global and Regional Europe | 1 Jan 1993 to 14 Jun 2024 | SEALEVEL_GLO_PHY_L3_MY_008_062 ( https://doi.org/10.48670/moi-00146) | -Geostrophy,
-Long Wave Length error -Barotrope -Equatorial waves (TIW, Pincaré waves) |
None |
The computation of L4 products uses the upstream 5Hz L3 SLA field, filtered and subsampled specificaly for the mapping.
In the REP/DT processing, the products can be computed optimally with a centred computation time window of ±6 weeks around the date of the map to be computed.
In the NRT processing, contrary to the REP/DT case, the products cannot be computed with a centred computation time window: indeed, as the future data are not available yet, the computation time window is not centred. Only data over the period the last 7 weeks to D ([D – 7 weeks, D]) are used, where D is the date of the production considered. For each day of NRT production, three merged maps are produced daily and delivered to the users (figure):
- A 0-day delay (i.e., map centred on day D), which represents a preliminary map production
- A 3-day delay (i.e., map centred on day D – 3 days), which represents an intermediate map production. When available, this map replaces the 0-day delay map
- A 6-day delay (i.e., map centred on day D – 6 days), which represents a final NRT map production. When available, this map replaces the 3-day delay map
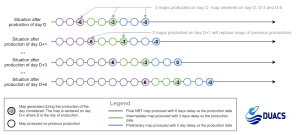
Figure : L4 product generation, NRT production. Three merged maps are produced daily and delivered to the users: final map (D – 6: 6-day delay), intermediate map (d-3: 3-day delay) and preliminary map (d0: 0-day delay).Both for the REP and NRT, the maps are dated on mid-night.
Note however that the spatial and temporal scales of the variability that is resolved in the DUACS merged products data set are imposed by the temporal correlation function used in the mapping procedure, as described in Pujol et al (2016) and Ubelmann et al., (2021).
It’s important to note that, in the polar regions, the sea-level anomaly provided by the MIOST mapping algorithm is derived through extrapolation, as no local altimeter data from leads are used to constrain the maps. Therefore, users should disregard gridded data in these areas and instead rely on the sea-ice mask included in the products.
Number of satellites to compute the maps
Both in REP/DT and NRT processing, the maps are computed with all the satellites available. This allows an improved signal sampling when more than two altimeters (corresponding to the minimal constellation) are available. The mesoscale signal is indeed more accurately reconstructed during these periods (Pascual et al, 2006), when omission errors are reduced by the altimeter sampling. The all-sat-merged series is however not homogeneous in time due to the evolutions of the altimeter constellation (see section Acquisition and data selection).
Formal mapping error
The formal mapping error does not represent the precision of the SLA gridded products, but it represents an excellent indicator of the consistency of the grid. The formal error variance should correspond to a local minimum in the least squares senses i.e. minimizes deviations from the mean. However, due to the computational cost and the wavelet-based formulation of the MIOST mapping approach, the error estimation method had to be revised for MIOST to deliver a global estimation of the formal error. In the MIOST products, the formal mapping error is determined using an ensemble approach. Specifically, an ensemble of 20 gridded product members is generated, each with a perturbed covariance model and observations. The standard deviation of the sea level anomaly (SLA) estimations across these ensemble members represents the formal mapping error.
In practice, the formal mapping error obtained depends on the constellation sampling capability (i.e. spatial distribution and density of the data used in the suboptimal estimation) and its consistency with the spatial/temporal scales and sea surface variability considered. But also on the noise budget for the different measurements used. The formal mapping error is usually low under the tracks of the different altimeters used in the mapping. It is higher within the inter-track diamonds. Higher formal mapping error is also observed over high variability areas.
The formal error for geostrophic currents is directly deduced from the SLA formal error matrix, by linearly combining diagonal and non-diagonal terms, follows the centered finite difference discretization.
L4 derived variables generation
The L4 derived variables consist of the Absolute Dynamic Topography (ADT) (maps and along-track) and maps of geostrophic currents (absolute and anomalies).
The ADT variable is obtained by adding a Mean Dynamic Topography (MDT) to the SLA field. The MDT used in the DUACS reprocessing is described in section Homogenization and cross-calibration.
The anomaly of the geostrophic current disseminated to users is derived from gridded SLA field. It is computed using a 3-point stencil width methodology Arbic et al., (2012) for latitudes outside the ± 5°N band. In the equatorial band, the Lagerloef methodology Lagerloef et al., (1999) introducing the β plane approximation is used. The absolute geostrophic current is obtained by adding to this anomaly the mean geostrophic current associated with the MDT field previously used.